Lookup tables are a common logic pattern in decision models. To model them, I have found that beginners naturally gravitate to decision tables, being the most familiar type of value expression. But decision tables are almost never the right way to go. One basic reason is that we generally want to be able to modify the table data without creating a new version of the decision model, and with decision tables you cannot do that. Another reason is that decision tables must be keyed in by hand, whereas normal data tables can be uploaded from Excel, stored in a cloud datastore, or submitted programmatically as JSON or XML.
The best way to model a lookup table is a filter expression on a FEEL data table. There are several ways to model the data table - as submitted input data, a cloud datastore, a zero-input decision, or a calculated decision. Each way has its advantages in certain circumstances. In this post we'll look at all the possibilities.
As an example, suppose we have a table of available 30-year fixed rate home mortgage products, differing in the interest rate, points (an addition to the requested amount as a way to "buy down" the interest rate), and fixed fees. You can find this data on the web, and the rates change daily. In our decision service, we want to allow users to find the current rate for a particular lender, and in addition find the monthly payment for that lender, which depends on the requested loan amount. Finding the lender's current rate is a basic lookup of unmodified external data. Finding the monthly payment using that lender requires additional calculation. Let's look at some different ways to model this.
We can start with a table of lenders and rates, either keyed in or captured by web scraping. In Excel it looks like this:
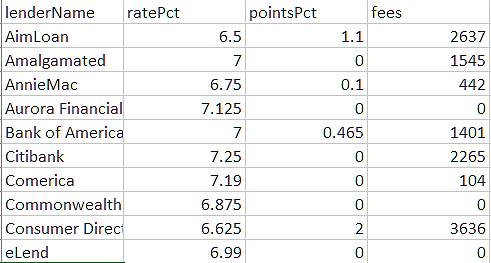
When we import the Excel table into DMN, we get a FEEL table of type Collection of tBankrate, shown here:
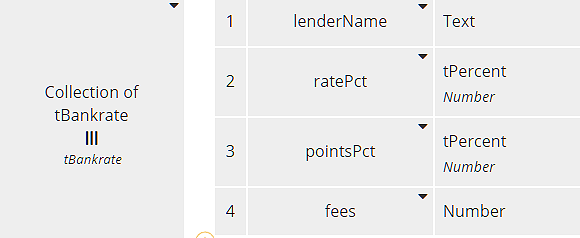
Each row of the table, type tBankrate, has components matching the table columns. Designating a type as tPercent simply reminds us that the number value represents a percent, not a decimal.
Here is one way to model this, using a lookup of the unmodified external data, and then applying additional logic to the returned value.
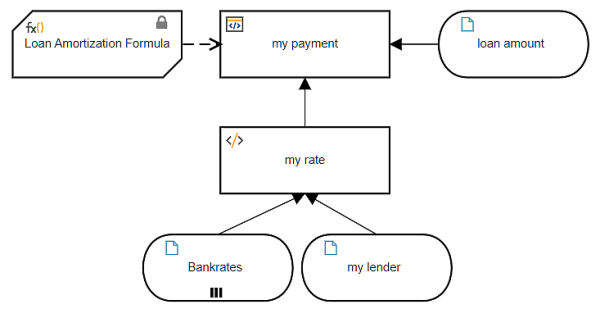
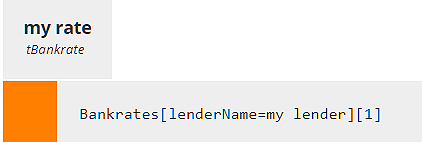
We define the input data Bankrates as type Collection of tBankrate and lookup my rate - the one that applies to input data my lender. The lookup decision my rate uses a filter expression. A data table filter typically has the format
<table>[<Boolean expression of table columns>]in which the filter, enclosed in square brackets, contains a Boolean expression. Here the table is Bankrates and the Boolean expression is lenderName = my lender. In other words, select the row for which column lenderName matches the input data my lender.
A filter always returns a list, even if it contains just one item. To extract the item from this list, we use a second form of a filter, in which the square brackets enclose an integer:
<list>[<integer expression>]In this case, we know our data table just has a single entry for each lender, so we can extract the selected row from the first filter by appending the filter [1]. The result is no longer a list but a single row in the table, type tBankrate.
The decision my payment uses a BKM holding the Loan Amortization Formula, a complicated arithmetic expression involving the loan principal (p), interest rate (r), and number of payments (n), in this case 360.

Decision my payment invokes this BKM using the lookup result my rate. Input data loan amount is just the borrower's requested amount, but the loan principal used in Loan Amortization Formula (parameter p) also includes the lender's points and fees. Since pointsPct and ratePct in our data table are expressed as percent, we need to divide by 100 to get their decimal value used in the BKM formula.
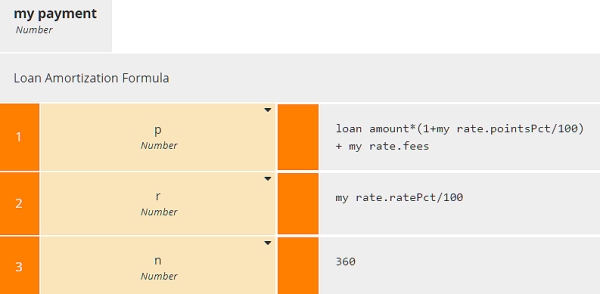
When we run it with my lender "Citibank" and loan amount $400,000, we get the result shown here.
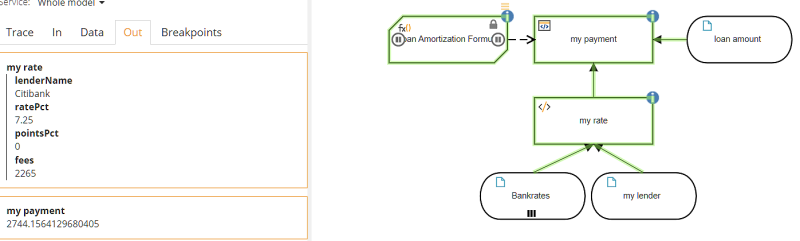
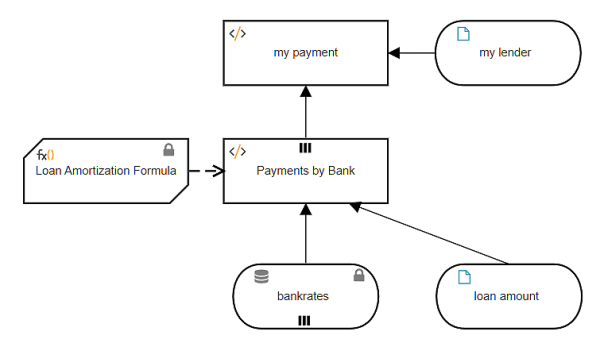
That is one way to do it. Another way is to enrich the external data table with additional columns, such as the monthly payment for a given loan amount, and then perform the lookup on this enriched data table. In that case the data table is a decision, not input data.
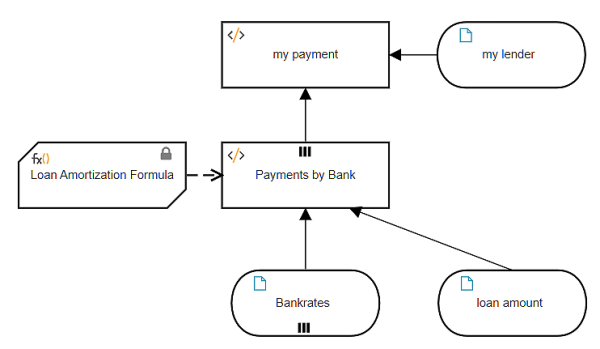
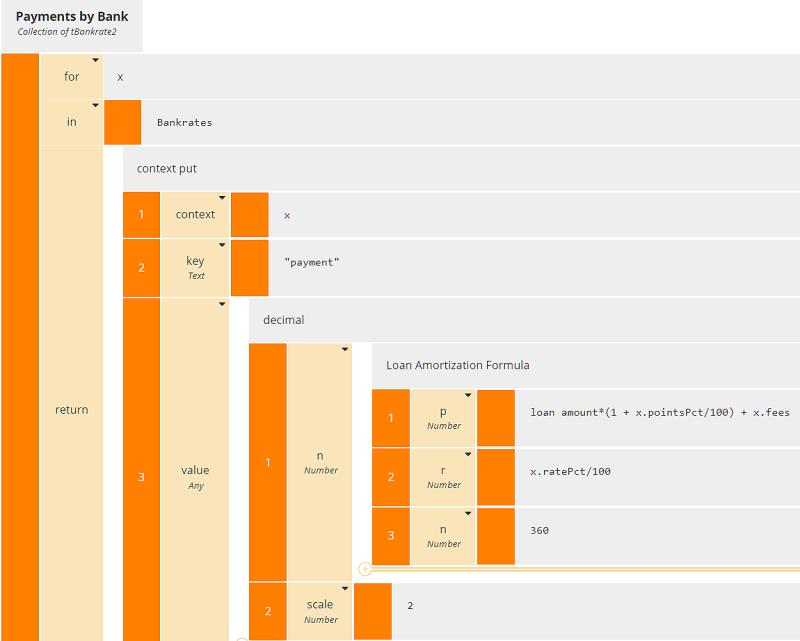
Here the enriched table Payments by Bank has an additional column, payment, based on the input data loan amount. Adding a column to a table involves iteration over the table rows, each iteration generating a new row including the additional column. In the past I have typically used a context BKM with no final result box to generate the each new row. But actually it is simpler to use a literal expression with the context put() function, as no BKM is required to generate the row, although we still need the Loan Amortization Formula. (Simpler for me, but the resulting literal expression is admittedly daunting, so I'll also show you an alternative way using boxed expressions that breaks it into simpler pieces.)
context put(), with parameters context, keys, and value, appends components (named by keys) to a an existing structure (context), and assigns their value. If keys includes an existing component of context, value overwrites the previous value. Here keys is the new column name "payment", and value is calculated using the BKM Loan Amortization Formula. So, as a single literal expression, Payments by Bank looks like this:
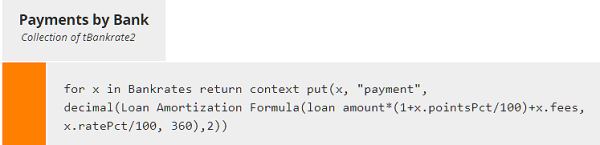
Here we used literal invocation of the BKM instead of boxed invocation, and we applied the decimal() function to round the result.
Alternatively, we can use the iterator boxed expression instead of the literal for..in..return operator and invocation boxed expressions for the built-in functions decimal() and context put() as well as the BKM. With FEEL built-in functions you usually use literal invocation but you can use boxed invocation just as well.
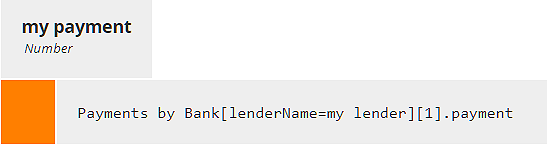
Now my payment is a simple lookup of the enriched data table Payments by Bank, appending the [1] filter to extract the row and then .payment to extract the payment value for that row.
When we run it, we get the same result for Citibank, loan amount $400,000:
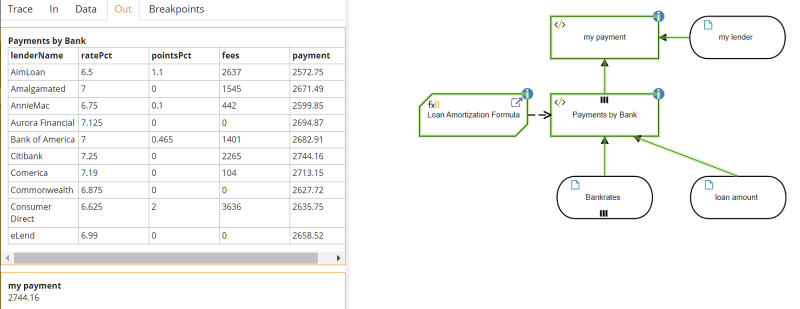
The enriched data table now allows more flexibility in the queries. For example, instead of finding the payment for a particular lender, you could use a filter expression to find the loan product(s) with the lowest monthly payment:
Payments by Bank[payment=min(Payments by Bank.payment)]which returns a single record, AimLoan. Of course, you can also use the filter query to select a number of records meeting your criteria. For example,
Payments by Bank[payment < 2650]will return records for AimLoan, AnnieMac, Commonwealth, and Consumer Direct.
Payments by Bank[pointsPct=0 and fees=0]will return records for zero-points/zero-fee loan products: Aurora Financial, Commonwealth, and eLend.
Both of these methods require submitting the data table Bankrates at time of execution. Our example table was small, but in real projects the data table could be quite large, with thousands of rows. This is more of a problem for testing in the modeling environment, since with the deployed service the data is submitted programmatically as JSON or XML. But to simplify testing, there are a couple ways you can avoid having to input the data table each time.
You can make the data table a zero-input decision using a Relation boxed expression. On the Trisotech platform, you can populate the Relation with upload from Excel. To run this you merely need to enter values for my lender and loan amount. You can do this in production as well, but remember, with a zero-input decision you cannot change the Bankrates values without versioning the model.
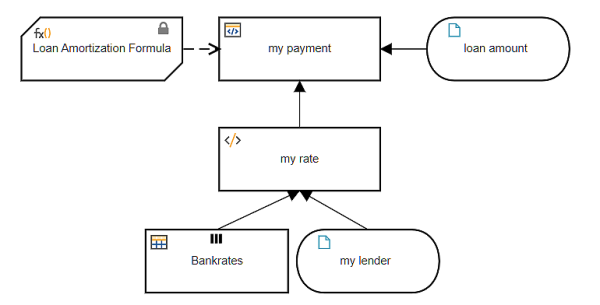
Alternatively, you can leave Bankrates as input data but bind it to a cloud datastore. Via an admin interface you can upload the Excel table into the datastore, where it is persisted as a FEEL table. So in the decision model, you don't need to submit the table data on execution, and you can periodically update the Bankrates values without versioning the model. Icons on the input data in the DRD indicate its values are locked to the datastore.
Lookup tables using filter expressions are a basic pattern you will use all the time in DMN. For more information on using DMN in your organization's decision automation projects, check out my DMN Method and Style training or my new book, DMN Method and Style 3rd edition, with DMN Cookbook.
